找到
2
篇与
短波通信
相关的结果
-
对短波通信选频的思考 0 前言 最近几年接触并参与了几个短波通信选频的项目，从算法实现到服务界面设计，都有过深度参与的经历。但受限于各种因素，每次的设计在我看来都不是那么的完善和人性化。基于自己的经验和一些思考，简单谈下自己的一些认知和想法。 1 什么是短波通信选频 1.1 简要背景 1901年古列尔莫·马可尼（Guglielmo Marconi）首次实现跨洋通信的壮举，直接推动了无线通信技术的发展与实用化。随着现代对电离层反射的研究，短波（3–30 MHz）因F层反射效率高、损耗低，成为跨洋通信的主流频段。 1.2 简要原理 短波通信实际上是利用地面-电离层形成的类似波导管的结构，使得电磁波在电离层和地面之间来回反射，从而传播到几百甚至上千公里的距离。 1.3 选频场景 可以用以下两种场景覆盖选频的需求 当我们知道发射站、接收站位置以及电离层参数信息时，我们就可以通过理论或经验公式计算得到两地之间的可通频率范围，从而再根据理论或经验计算得到最佳的通信频率。 当我们知道发射站位置、通信频率以及电离层参数信息时，我们就可以通过理论或经验公式计算该频率可以传播到的空间范围，再根据损耗等参数信息，得到当前通信频率的最佳通信位置区间。 1.4 需要哪些技术和数据 电磁波传播路径计算：射线追踪技术、QPS模型下的传播路径公式、马丁等效原理、国际电联组织（ITU-R）提供的经验公式等 用途：根据站点位置、通信频率、电离层参数等信息，理论计算或经验估算电磁波的传播路径，从而判断当前频率是否有效 比较：从我的经验来看，以上这些技术所提供的结果不会有太大的区别，通常来说选择一种即可 成熟度：以上这些技术都比较成熟 电磁波损耗计算：这一块目前我只使用过ITU-R提供的经验公式进行过计算 用途：辅助判断电磁波的损耗是否严重，具体哪个可通频率的损耗最小 成熟度：在ITU-R官方文档中可查询，比较成熟 电离层参数：根据使用的技术不同，需求的具体参数也不同 射线追踪：通信时刻的三维电离层网格化数据（经度$\times$纬度$\times$高度） QPS模型下的传播路径公式：通信时刻的三维电离层网格化数据（经度$\times$纬度$\times$高度） 马丁等效原理：通信时刻反射点位置的电子密度剖面（若需要计算任意链路，约等于需要通信时刻的三维电离层网格化数据） ITU-R：通信时刻反射点位置的foF2、foF1、foE和M(3000)F2（若需要计算任意链路，约等于需要通信时刻前述各个参数的二维Map数据） 重要程度：由于选频技术已经非常成熟且区别不会很大，所以输入数据的好坏是影响选频结果好坏的关键所在。好的数据才能产出好的结果，差的数据什么技术也不好使。 分类：在应用场景，经常会出现现报和预报，选频的现报和预报则只与数据的现报和预报有关。现报：通常利用探测设备实时探测的电离层参数信息，实时同化处理成所需要的三维或二维电离层网格化数据，由于数据处理的复杂性，必然会存在一定的时间延迟；预报：通常利用已有的电离层模型，通过改变输入时间等参数，让模型输出所需要的三维或二维网格化数据，众所周知，目前的电离层模型准确度都不够高，所以预报结果只会是一个大致的估算结果，在电离层平静期可能不会有较大差距。 成熟度：无论哪种技术，对电离层参数的需求基本都是通信时刻全球（或重点区域）的三维或二维网格化数据。即便是现报，由于电离层探测设备不可能全空间覆盖，生成指定时刻准确的三维或二维网格化数据也是一件非常困难的事情。 2 工程化技术的选择 虽然前面提到了电离层三维网格化数据获取的困难性，但在一定误差范围内还是能做一些事情的。 2.1 选频技术的选择 首先，个人对纯经验模式是没那么推崇的，虽然可能效果短期内看起来还不错，但上限很有限且不够物理，所以排除ITU-R经验公式和马丁等效定理；其次，工程化过程中计算效率非常重要，过于复杂而导致时效性很差是得不偿失的，所以排除射线追踪技术（叠甲：对于优化很好、计算效率很高的射线追踪代码，肯定是优先考虑的）。那么就只剩下了QPS模型下的传播路径计算公式。 QPS模型是将电子密度剖面分为一段一段的抛物线，通过最小二乘拟合，得到一组最符合实际剖面的分段解析公式。将电子密度剖面解析的目的是对电磁波传播路径进行积分计算时，方便积分得到解析解。 QPS模型是上世纪提出的方法，从我目前的认知来看，或许完全不需要弄得这么复杂，当前数值方法很多且很成熟，直接使用数值解可能会更加的简单有效。2.2 电离层参数的获取 现报 对于存在观测数据的情况，对观测数据进行同化处理，得到三维或二维网格化数据是一种很容易想到的方向。我对同化技术没有过研究，只了解之前项目用过的一种非常简单的方法。不过，同化技术已经发展了很多年，应该是有很多比较成熟的论文可以参考的。 预报 从我的经验来看，预报往往才是用户最想要的内容。很多时候，我们都是想提前知道未来某个时刻的通信状况如何。但这一点却是这个工程中最难的一点。 一种比较简单的处理方法是直接使用某个电离层模型未来时刻的输出作为对电离层参数的预报，这个方法在之前的项目中采用了很多次。 另外一种可能的方法是利用已有的电离层参数信息，采用深度学习等手段，训练生成未来时刻的电离层参数，就是不清楚对于三维空间网格，这种方法的难度和计算量会不会太大。 还有一种可能的方法是通过预报电离层模型输入参数，然后利用预报的模型输入参数驱动模型，从而生成预报的电离层参数，但我也从未对此进行过研究和调研。 结合现报的一种可能方法是通过预报观测台站位置的电离层数据，得到预报的台站数据，然后利用现报的同化模型，使用预报的台站数据同化得到预报的三维或二维网格化电离层参数。 2.3 选频结果 短波通信计算中有很多频率，如最大可用频率（MUF）、最低可用频率（LUF）、最高可能频率（HPF）、最佳工作频率（OWF）等，从我的经验来看，计算MUF和LUF就足够了，太多的频率参数反而会让用户很困惑。 除了频率外，大圆距离、传播模式、时延、损耗等也是比较重要的信息，能提供一定的辅助判断，最好也是能够输出的。 3 界面设计及展示思路 3.1 选频界面 对于1.3节中提到的第一个选频场景，可以设计如下界面： 通信时间：能够选择到某一天即可，不需要具体到时刻 发射站位置：可以直接输入经纬度坐标，也可以在地图中选点 接收站位置：可以直接输入经纬度坐标，也可以在地图中选点 开始计算：点击后，将上述表单信息传递给后端算法处理，自动计算通信时间那一天24h所有时刻的选频结果，时间分辨率最低1小时最高15分钟即可 折线图展示框：横坐标0至24h，纵坐标频率，折线图展示计算结果即可。如果能够计算损耗，采用二维彩图的形式将LUF到MUF之间的损耗或信噪比展示出来，效果会更好。 一次性计算24h的选频结果参考了VOACAP的设计思路，同时选频有明显的日变化，一天的数据也更有利于展示，使展示结果更加的美观。 对于现报和预报的区分，我觉得不需要在界面上显示出来，设定好时间后，让后台算法自动区分识别即可，这种处理可以避免前端过多冗余、复杂的选项。 3.2 指定频率传播范围 对于1.3节中提到的第二个选频场景，可以设计如下界面： 通信时间：需要具体到某个时刻，与电离层数据的时间分辨率有关（如30分钟） 通信频率：指定某个通信频率，3～30MHz之间 发射站位置：可以直接输入经纬度坐标，也可以在地图中选点 开始计算：点击后，将上述表单信息传递给后端算法处理，自动计算通信时间发射站向四周辐射的选频结果 二维地图展示：以发射站为中心，展示四周可通信范围，大致应该是个环状结构。如果可以计算损耗或信噪比，则对可通范围进行上色处理，效果会更好。 3.3 小结 个人觉得选频界面有上面两个就足够了，当然也可以根据需求自定义一些界面，如典型链路、电离层参数展示等界面。 4 后记 短波通信选频很多时候可能并不能够满足用户的所有需求，还需要一些对短波通信环境判断的辅助手段，如根据太阳活动、地磁活动等数据的反应，分析处理成一份有一定时效性和简单易懂结论的报告或指数。之前也参与了一部分相关内容的项目，也有一些思考和想法，以后有时间再写一写。 个人觉得研究应该是带着解决某个问题或疑问的目的去进行的，最终结果应该是实实在在的为某个问题的解决提供了帮助，或者解开了心中对未知领域的部分疑惑。过于追求新颖、独特，带来的未必就是有用的、有效的、实在的内容。 记得初中有一次数学课，老师讲解证明两个直角三角形全等的问题（已知斜边和直角边相等），给了两种证明方法。激发了不少同学提出新解法的兴趣，然后大家一起提出了好几种证明过程复杂且冗余的方法（我贡献了两三个= =），比如先用勾股定理计算另外一条直角边，再通过arctan计算斜边旁边的一个角，然后通过SAS证明全等。作为一时思考的乐趣固然很有意思，但从实际角度来说，HL定理已经是前人总结后最简单有效的方法了。
-
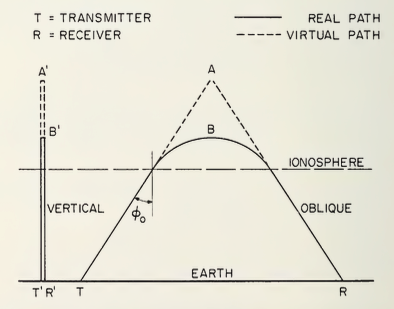
高频传播特性的等效关系 0 前言 短波通信是一种常见的通信方式，其利用高频（High Frequency，HF）电磁波在电离层和地面之间的一次或多次反射，最远可将信号传至上万公里。在这个过程中，可以认为电离层和地面形成了类似“波导管”的结构。 在短波通信中，为了简化计算，通常会使用一些等效关系，这里将根据参考文献[1]中的内容，对这些等效关系进行介绍。 1 平面地球和平面电离层 1.1 “割线定律” - The "Secant Law" 在本节中，我们将考虑两个波的频率、虚拟路径和吸收之间存在的关系，一个波以斜入射反射，另一个波以垂直入射反射，二者的反射发生在相同的真实高度。为此，考虑以如下图所示的角度入射到平面电离层上的射线，其中电子密度随高度增加，从而发生全内反射。 WX20230914-164703图片 Refs [1] 图4.1 平面地球与平面电离层的等效定理在没有碰撞和外加磁场的情况下，在等离子体频率为$f_N$的水平高度上，频率为$f$的波的折射率$\mu$由下式给出： $$ \mu^2 = 1 - \left( \frac{f_N}{f} \right)^2 \tag{1} $$在反射层应用斯涅尔定律（Snell's law），即$\mu = \sin \phi_0$，可知 $$ f_N = f \cos \phi_0 $$如果$f_\nu$是与斜入射频率$f$在相同的真实高度（即相同的等离子体频率）上以垂直入射反射的频率，则$f_\nu =f_N$。因此 $$ f_\nu = f \cos \phi_0 \qquad {\rm or} \qquad f = f_\nu \sec \phi_0 \tag{2} $$该频率称为“等效垂直入射频率”，对应于$f$。上式中第二个式子就是所谓的割线定律。上述结果表明，在斜入射下，电离层反射的频率比正常入射时高得多。 1.2 Breit和Tuve定理 - Breit and Tuve's Theorem 另一个比较重要的关系称为Breit和Tuve定理。其中表示发射机T与接收机R之间传输的群（或等效）路径$P'$由等效三角形TAR的长度给出，即： $$ P' = TA + AR \tag{3} $$这可以通过以下论证来证明： $$ P' = \int_{TBR} \frac{ds}{\mu} = \int \frac{dx}{\mu \sin \phi} = \frac{1}{\sin \phi_0} \int dx = \frac{TR}{\sin \phi_0} = TA + AR $$请注意，反射的真实高度B总是小于A处的等效高度。 应该记住，只有当发送者和接收者位于电离层之外时（3）式才成立。如果发射机和接收机位于电离层内，即折射率为$\mu_1$的水平高度上，则（3）式的右侧必须除以$\mu_1$，这样$P'$仍然意味着群传播时间乘以自由空间速度。 1.3 马丁（等效路径）定理 - Martyn's (Equivalent Path) Theorem 如果$f$和$f_\nu$是从同一实际高度斜向和垂直反射的波的频率，则垂直反射信号的虚高等于斜向信号的等效三角路径的高度。 考虑等离子体频率为$f_N$的相同实际高度下，斜波和垂直波的折射率为$\mu_{ob}$和$\mu_\nu$，我们有 $$ \mu_{ob}^2 = 1 - \left( \frac{f_N}{f} \right)^2 \qquad {\rm and} \qquad \mu_\nu^2 = 1 - \left( \frac{f_N}{f \cos \phi_0} \right)^2 \tag{4} $$根据斯涅尔定律（Snell's law）可知$\mu_{ob} \sin \phi = \sin \phi_0$。联立这些方程可以得到 $$ \mu_{ob} \cos \phi = \mu_\nu \cos \phi_0 \tag{5} $$斜测信号的群路径为 $$ P' = \int_{TBR} \frac{ds}{\mu_{ob}} = 2 \int_0^{h_r} \frac{dh}{\mu_{ob} \cos \phi} = \frac{2}{\cos \phi_0} \int_0^{h_r} \frac{dh}{\mu_\nu} = \frac{2}{\cos \phi_0} h_\nu' $$其中 $$ h_\nu' = \frac{1}{2} P' \cos \phi_0 = \frac{1}{2} (TA + AR) \cos \phi_0 = AD $$因此 $$ P'(f) = h'(f_\nu) \sec \phi_0 \tag{6} $$这个定理表达了斜入射波的虚反射高度与等效垂直波的虚反射高度相等的重要关系。 1.4 马丁（吸收）定理 - Martyn's (Absorption) Theorem 略。 $$ \tag{7} $$$$ \tag{8} $$2 电离层曲率的影响 WX20230914-173108图片 Refs [1] 图4.2 斜入射射线几何图像在弯曲的电离层中，斯涅耳定律的形式是 $$ \mu r \sin i = \mu_0 r_0 \sin i_0 \tag{9} $$式中$r$为从地心到折射率为$\mu$处的半径矢量的长度，半径矢量与光线夹角为$i$，如上图所示，图中$\mu_0$、$r_0$和$i_0$为任意参考值。以地面为参照，则有$\mu_0 = 1$、$r_0 = a$且$i_0 = (\pi/2) - \Delta$，其中$\Delta$为仰角。即 $$ \mu r \sin i = a \cos \Delta \tag{10} $$将式（1）代入式（10），使用$f_\nu$替换$f_N$，给出了频率$f$与相同实际高度$h_r$反射的等效垂直频率$f_\nu$之间的关系。即 $$ \left( \frac{f_\nu}{f} \right)^2 = 1 - \left( \frac{a \cos \Delta}{a + h_r} \right)^2 \tag{11} $$设$\phi_r'$为未折射光线的延线与半径矢量在$h_r$处的夹角，如上图所示。从几何关系中可以得到 $$ (a + h_r) \sin \phi_r = a \cos \Delta \tag{12} $$因此 $$ f_\nu = f \cos \phi_r \tag{13} $$由式（11）和式（13）可以看出，等效频率不仅与$\Delta$有关，而且与反射高度$h_r$有关。 $f_\nu$可以用（6）式或（7）式来定义，而不是用反射高度来定义，但与平面电离层的情况不同，$f_\nu$的值将取决于定义。 参考 [1] Ionospheric radio propagation
